Back in 2011, Marc Andreessen told us “Software is eating the world.” Now, more than a decade later, there’s a new guest at the table, and “AI is eating software.” More products and processes, including the creation of software itself, are being powered by advanced Machine Learning.
But Machine Learning shouldn't just ingest and create haphazardly. To build a good ML-powered system, you have to overcome two common problems: organizing your data in a way that lets you quickly retrieve relevant information, and, relatedly, representing your data in a way that makes it easy to feed into your ML models.

These two problems are related. Indeed, they converge as parts of what is, in essence, the defining challenge of many ML systems: turning your data into vector embeddings – that is, connecting your Data Sources to your Vector Search & Management system.
We call this the Vector Compute problem and this article explores how to build & use systems that solve it.
In basic terms, Vector Compute is the infrastructure responsible for the training and management of vector embedding models, and the application of these models to your data in order to produce vector embeddings. These vectors then power the information retrieval and other machine learning systems across your organization.
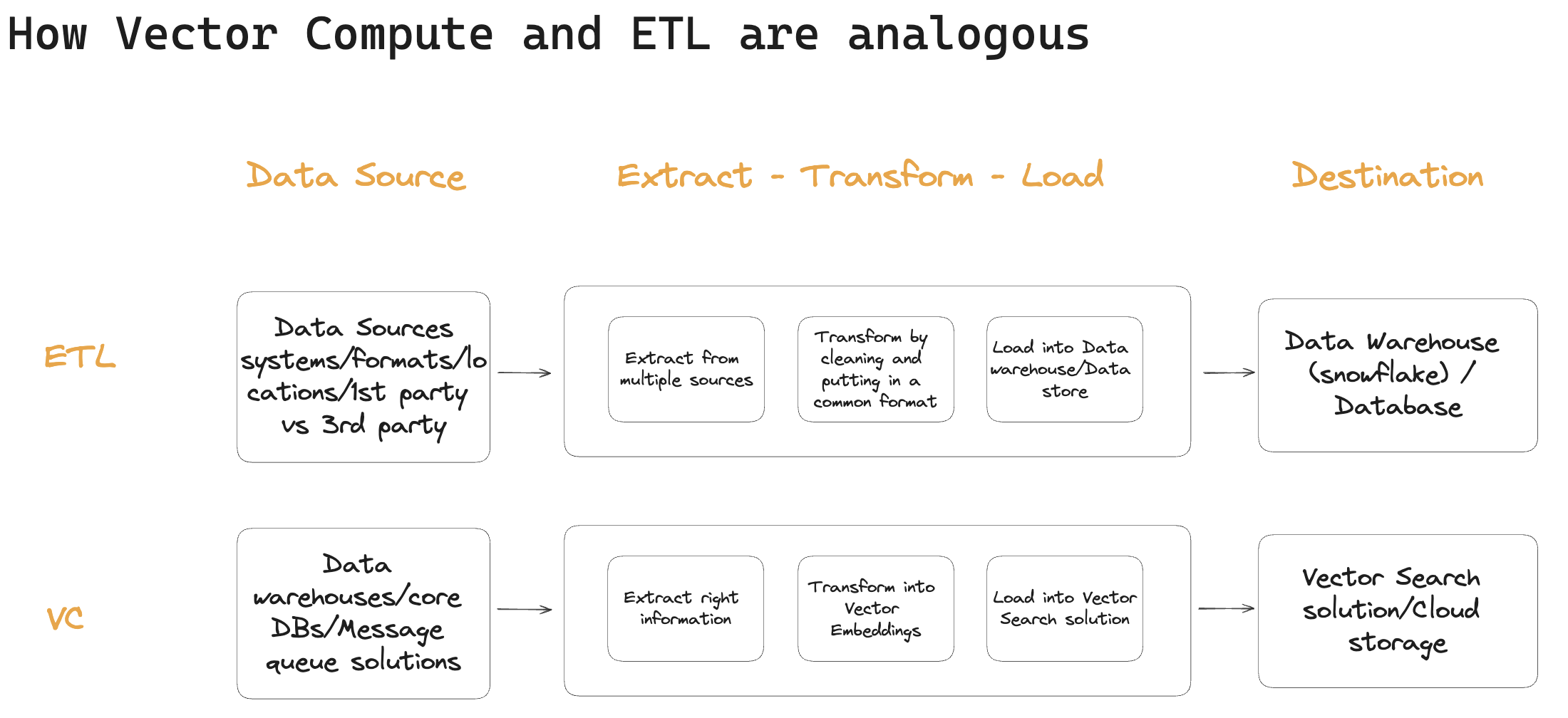
The role Vector Compute fills for your information retrieval system is similar to the role ETL tools like fivetran fill for your data warehouse. As in ETL, in Vector Compute you have to Extract the right information, Transform it into Vector Embeddings, and Load it into your Vector Search solution or cloud storage.
There are, however, two important distinctions between ETL and Vector Compute:
Your ETL system has to interact with dozens of data sources - loading data from all kinds of messy places, focusing on cleaning it up, setting and validating a schema, and keeping everything as simple as possible while the data landscape of your company changes, over time. In contrast, the data sources that feed into your Vector Compute stack are likely those used as destinations by your ETL systems, like the data warehouse, your core database, or message queue solution. This means there can be fewer sources in Vector Compute and they are likely of higher quality.
The transform step in ETL often contains just a simple aggregation or a join, or it fills in a missing value from a default. These operations are easy to express in SQL, making it easy to test whether they work. In Vector Compute, on the other hand, we convert a diverse set of data into vector embeddings, which is a machine learning problem rather than a pure data engineering problem. This means that Vector Compute takes much longer to build than a simple ETL pipeline, more resources to run because you’re using ML models, and is more difficult to test – ML models don’t follow a simple “if A then B” logic, but instead operate within a spectrum of evaluation that is variable and task-specific.
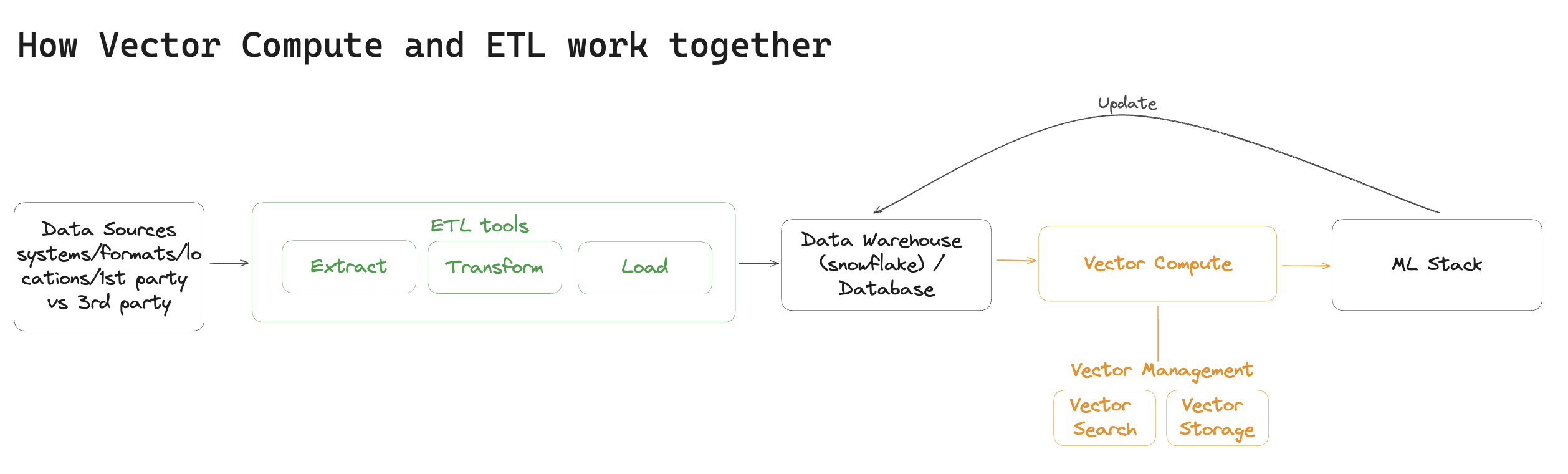
In short, Vector Compute uses the data delivered by the ETL stack as input and transforms it into vector embeddings, which are then used to organize the data and extract insight from it.
Finally, the key challenge you will face when building a Vector Compute system is developing and configuring embedding models.
Now let's dive into the details.
At the core of Vector Compute are embedding models – machine learning models applied to raw data to generate vector embeddings.
Embedding models turn features extracted from high-dimensional data, with large numbers of attributes or dimensions, like text, images, or audio, into lower-dimensional but dense mathematical representations – i.e., vectors. You can apply embedding models to structured data like tabular datasets or graphs.
Read more about embedding models, here
Your task's unique requirements will dictate when you should use a custom model, and when you should use a pre-trained model.
Read more about how to choose the right type of model for your use case, here
So what does this all mean? Such robust homegrown solutions will be increasingly important given the broad and ever-expanding application of Vector Compute to solve real-world problems in a spectrum of domains, partially discussed here.
Stay updated with VectorHub